A micro-course in magnetism: Magnetic Field created by Current Carrying Wires and solenoid, Magnetic Force Between Two Parallel Conductors, Magnetic Flux and Faraday’s Law of Induction and Lenz’s Law, and Self-Induction, for high school students.
Magnetic Field created by a Current Carrying Wire
A moving electric charge creates magnetic field in space in addition to the electric field. So the current carrying wire creates magnetic field in space.
Magnetic field created by a long, straight charge carrying wire.
At any given point in space, the magnitude of magnetic field created by the infinitely long, straight wire carrying a direct current 'I', is inversely proportional to the distance from the wire, and directly proportional to the electric current, i.e.,
where 'r' is the distance from the wire, and μ0 is the permeability of the free space (or vacuum). The permeability of air can be approximated by μ0.
The value of μ0 is given by,
μ0 = 4π × 10-7
Magnetic Field of a Current Loop
If the electric current is moving on a circular loop, the magnetic field created by it in space is more stronger inside the loop than the outside the loop.
Magnetic field created by a circular current loop.
Magnetic field intensity at the center of the circular loop is given by,
where 'I' is the electric current on the circular wire (loop), and 'R' is the radius of circle.
Inductors
Inductor is a electronic component that stores energy as the form of magnetic energy in its magnetic field. The more stronger the magnetic field is the more energy will be stored. A wire loop is a simplest form of inductors, but a coil or a solenoid are inductors able to store more energy in their magnetic fields.
For a coil of 'N' turns, electric current on the loop is 'NI' where 'I' is the electric current supplied to the coil. So the magnetic field inside the coil and at the center of it is given by,
So by raising the number of turns, the magnetic energy stored inside the loop is increasing.
Magnetic field of a solenoid
Solenoid is a long straight coil of wire which can be used to generate a nearly uniform magnetic field.
Magnetic field created by a solenoid.
Magnetic field outside the solenoid is very week. But if the solenoid is infinitely long, magnetic field inside it, is uniform and is given by this equation,
where 'n' is the number of turns per unit length of the solenoid. This is a good approximation to the field inside a solenoid far away from the edges of the solenoid.
If the medium inside the solenoid is something other than air (or vacuum), the magnetic field inside it will be given by,
where 'k' is the relative permeability of the medium inside the solenoid, where permeability of the medium is, μ = kμ0.
Magnetic field of an iron core solenoid is more stronger than air core solenoid, due to the higher permeability of iron.
Magnetic Force Between Two Parallel Conductors
In previous sections we saw that a moving electric charge (or a current carrying wire) creates magnetic field in space, and also magnetic field in space exerts magnetic force to the moving electric charge (or a current carrying wire). So current carrying conductors will exert magnetic action/reaction forces to each other by creating magnetic field in space.We can find magnetic force between two straight, infinitely long conductors which are parallel to each other, and they are carrying direct electric currents, I1 and I2:
Magnetic force between two parallel conductors.
According to the picture above, magnetic field created by the first conductor carrying electric current I1 , is 'B', with magnitude of,
where 'd' is the distance from the conductor where I2 is flowing on the second conductor. So the magnitude of the force acting on length 'L' of the second conductor, by magnetic field 'B', is given by,
So we have,
This force is attractive if I1 and I2 are in the same direction, and it is repulsive if I1 and I2 are flowing in opposite directions.
Force acting by the second conductor on length 'L' of first conductor is also equal in magnitude but opposite to the direction of the force acting by the first conductor on length 'L' of the second one.
Magnetic Flux and Faraday’s Law of Induction and Lenz’s Law
Magnetic flux:Magnetic flux passing through a loop.
Inside a uniform magnetic field in space with intensity 'B' , magnetic flux passing through a loop is given by,
where the magnitude of vector 'A' in this equation is the surface area of loop, and its direction is the direction of the normal vector, 'N' that is normal to the surface of the loop. So Φ is a scalar quantity, and it is equal to,
Φ = BA cos(θ)
where the angle between 'B' and 'N' is θ, and 'A' is the surface area of the loop.
SI unit of magnetic flux is Weber (Wb), so one Weber per square meter is equal to one Tesla.
Faraday’s law of induction and Lenz’s law:
Faraday’s law: Variation of magnetic flux inside a conducting loop (e.g. a coil of a wire), induces electromotive force (voltage) on the loop. The variation of the magnetic flux may be caused by the change in the magnetic field, or the area of the loop, and etc... Induced electromotive force is equal to the rate of the change of the magnetic flux.
Lenz's law: Induced electromotive force in a conducting loop, produces a current whose magnetic field opposes the change which produces it. So the induced electromotive force is minus the rate of the change of the magnetic flux.
So the electromotive force induced on a conducting loop with 'N' turns, through the variation of magnetic flux inside loop, is given by,
The induced electric current in the loop is also given by,
where 'R' is the resistance of the loop.
Self-Induction
Change in electric current on a circuit, causes a change in magnetic field created by the current, and change in magnetic field induces electromotive force on the same circuit, and Self-induced emf (voltage) produces electric current whose magnetic field opposes the change in the magnetic field of the circuit. This phenomenon is called self-induction.Self-induced electromotive force on the circuit is directly proportional to the change in electric current over time, i.e.,
where 'L' is the proportionality constant, and it is called self-inductance. SI unit of 'L' is Henry (Hn).
Self-induction is more prevalent if there is a coil or solenoid on the electric circuit.
When current 'i' flows on a solenoid, with length 'l' and 'N' turns, the uniform, axial magnetic field created inside it, is given by,
So the magnetic flux passing thorough cross-sectional area 'A' of the solenoid, is given by,
So the self-inductance of solenoid is,
'L' depends on only the dimensions of the solenoid, and the number of turns. It also depends on the medium inside the solenoid (through this equation: μ = kμ0 ).
Energy stored in an inductor:
Energy stored in an inductor is given by,
So it depends on inductance and the current flowing through the inductor.
'W' is in fact the work done by a voltage source against emf force induced in inductor due to the change in electric current.













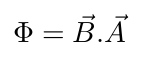

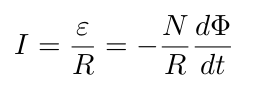






No comments:
Post a Comment
Note: Only a member of this blog may post a comment.