A micro-course in Gravity that is the section six of the course in classical mechanics available on Physics 12: Classical Mechanics. This course contains lectures on Newton's law of universal gravitation, fields of force, Kepler's laws of planetary motion, and satellite motion.
Newton's Law of Universal Gravitation
According to the Newton's law of universal gravitation, any two particles attract each other with a force that is proportional to the product of their masses and inversely proportional to the square of the distance between them. This law does not explain what gravity is, it only explains how the force of gravity works.
Position vectors of two point-like objects with masses of m1 and m2 , in a coordinate system with origin 'o', is given in this picture,
Gravitational force exerted by m1 on m2, is given by,
where,
is the proportionality constant (or universal constant).
Similarly, m2 exerts gravitational force on m1, given by,
and since,
we have,
This equation shows that, these two forces are action-reaction pair.
Fields of Force
If in a region of space, a force acts on a particle, there is a field of force in that region. Gravitational, electrical, and magnetic fields are examples of fields of force.
Gravitational field created by a point-like object with mass 'm', at a distance 'r' from it, is given by,
This equation is valid for spherically uniform distribution of mass 'm' inside a sphere with radius equal or less than 'r'.
Kepler's Laws of Planetary Motion
Kepler's laws of planetary motion are three laws which describe the motion of planets around the Sun.
-According to the first law, the law of orbits (or the law of ellipses), planets move in a elliptical orbits with the Sun at one focus of the ellipse.
-Second law (or the law of equal areas): A line from the Sun to a planet sweeps out equal areas during equal intervals of time, i.e.,
if t1=t2 then A1=A2
- Third law (or the law of period): the square of the period of a planet's revolution around the Sun is proportional to the cube of the semi-major axis of its orbit, i.e.,
where 'K' is a constant.
Satellite Motion
Gravitational force acting on a satellite in the gravitational field of Earth, provides a centripetal force responsible for the motion of satellite around the Earth. When satellite is moving on a circular orbit, its speed is constant, and it is in circular uniform motion.... Find more .
Problems and Solutions
Problem 1
At what point between the Earth and the Moon, the magnitude of the gravitational pull of the Earth is equal to the magnitude of the gravitational pull of the Moon?
Problem solving lecture in Gravity:1
Problem 2
The gravitational field intensity at the surface of a planet is 3.4 N/kg. If the planet's mass is 7.2*1022 kg. What is the radius of the planet?
Problem solving lecture in Gravity:2


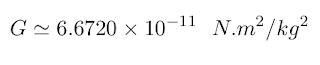






No comments:
Post a Comment
Note: Only a member of this blog may post a comment.